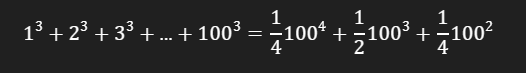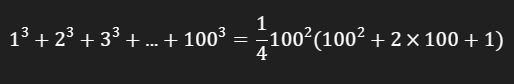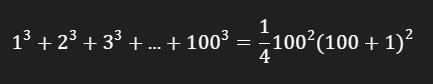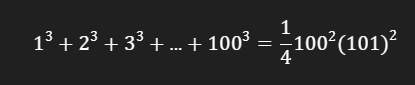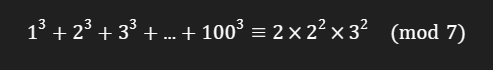Sisa pembagian 1³ + 2³ + 3³ + … + 100³ oleh 7 adalah…a. 1b. 2c. 3d. 4e. 5
Simplenews | Pernahkah Anda bertanya-tanya, apa sisa pembagian dari jumlah pangkat tiga bilangan bulat dari 1 sampai 100? Misalnya, jika kita menjumlahkan 1³ + 2³ + 3³ + … + 100³, lalu membaginya dengan 7, berapa sisanya?
Jawabannya ternyata cukup sederhana, yaitu 2. Bagaimana cara menemukannya? Mari kita lihat penjelasan berikut.
Konsep Dasar
Untuk menyelesaikan masalah ini, kita perlu mengingat dua konsep dasar, yaitu:
Rumus jumlah pangkat tiga bilangan bulat dari 1 sampai n, yaitu:
Sifat kongruen modulo, yaitu:
a≡b(modm)⟺a=b+km
di mana k adalah bilangan bulat.
Artinya, dua bilangan a dan b dikatakan kongruen modulo m jika mereka memiliki sisa yang sama jika dibagi dengan m.
Langkah Penyelesaian
Dengan menggunakan konsep-konsep di atas, kita bisa menyelesaikan masalah ini dengan langkah-langkah berikut:
Substitusikan n = 100 ke dalam rumus jumlah pangkat tiga bilangan bulat, sehingga kita mendapatkan:
Keluarkan faktor 100² dari setiap suku, sehingga kita mendapatkan:
Faktorkan suku dalam kurung, sehingga kita mendapatkan:
Perhatikan bahwa 100 + 1 = 101, sehingga kita bisa menulis:
Sekarang, kita ingin mencari sisa pembagian dari ekspresi di atas jika dibagi dengan 7. Untuk itu, kita perlu mencari nilai-nilai kongruen modulo 7 dari setiap faktor, yaitu:
Dengan menggunakan sifat kongruen modulo, kita bisa menulis:
Substitusikan nilai-nilai kongruen modulo 7 yang sudah kita temukan, sehingga kita mendapatkan:
Hitung nilai dari ekspresi di kanan, sehingga kita mendapatkan:
Cari sisa pembagian dari 72 jika dibagi dengan 7, sehingga kita mendapatkan:
Jadi, sisa pembagian dari jumlah pangkat tiga bilangan bulat dari 1 sampai 100 jika dibagi dengan 7 adalah 2.
Kesimpulan
Dari penjelasan di atas, kita bisa menyimpulkan bahwa:
- Sisa pembagian dari jumlah pangkat tiga bilangan bulat dari 1 sampai 100 jika dibagi dengan 7 adalah 2.
- Untuk menemukan sisa pembagian tersebut, kita perlu menggunakan rumus jumlah pangkat tiga bilangan bulat dan sifat kongruen modulo.
- Dengan menggunakan konsep-konsep tersebut, kita bisa menyederhanakan masalah ini menjadi masalah yang lebih mudah dihitung.
Penutup
Anda telah membaca artikel tentang sisa pembagian dari jumlah pangkat tiga bilangan bulat. Anda telah mempelajari rumus dan langkah-langkah penyelesaiannya dengan mudah dan cepat.
Anda juga telah mengetahui sumber dan referensi yang dapat Anda gunakan untuk memperdalam materi ini.
Jika Anda ingin belajar lebih banyak tentang matematika dan topik-topik lainnya, Anda bisa mengunjungi situs Simplenews.
Simple News memberikan Kunci Jawaban Tematik lengkap Terbaru. Tersedia pembahasan soal dan kumpulan kunci jawaban tematik sd/mi kelas 1 2 3 4 5 6, subtema 1 subtema 2 subtema 3 subtema 4 subtema 5 subtema 6, kegiatan berbasis proyek dan literasi, pembelajaran 1 pembelajaran 2 pembelajaran 3 pembelajaran 4 pembelajaran 5 pembelajaran 6 secara lengkap dan terbaru.